定义，范围不同。一.无限小数范围大于循环小数。无限小数包含循环小数。循环小数是无限小数，但无限小数不一定是循环小数。无限循环小数的位数是潜无穷而不能是实无穷。它本质上表示一个无限趋近于某个数字的小数形式。而无限小数又分无限循环小数与无限不循环小数两类

定义，范围不同。

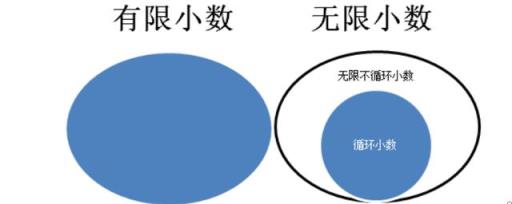
一.无限小数范围大于循环小数。无限小数包含循环小数。循环小数是无限小数，但无限小数不一定是循环小数。无限循环小数的位数是潜无穷而不能是实无穷。它本质上表示一个无限趋近于某个数字的小数形式。而无限小数又分无限循环小数与无限不循环小数两类。

二.“无限趋近”也就是变量，所以无限循环小数并不是一个精确的数字。换言之，“无限循环小数”并不是一个小数，它是一个函数，它无限趋近于某个数字。

三.无限不循环小数的存在是理论证明的，因为是不可能直接验证的。理论上是先证明：两个整数的商一定是有限小数或者无限循环小数。再证明每个无限循环小数都能用两个整数的商表示。接下来证明存在某个数不可能等于两个整数的商。那么这个数就一定不是有限小数或者无限循环小数。